“Algoritmalara giriş” kitabında marağımı çəkən bir məsələ ilə qarşılaşdım və blogda da paylaşmaq qərarına gəldim. Düzdür yazmaq çox əziyyətlidir, həm də xeyli vaxt aparır, amma avantajlarını nəzərə alanda əziyyətinə qatlaşmalı olursan.
Keçək məsələmizə. Fərz edin ki, siz səhm alqı-satqısı ilə məşğulsunuz. Səhmlərin növbəti 17 gün üçün qiymət proqnozları verilib. Bu 17 gün ərzində ancaq bir dəfə səhm ala və sata bilərsiniz. Ona görə də alış və satış günlərini elə seçməlisiniz ki, maksimum gəlir əldə edəsiniz.
Bunun üçün ticarətdə ənənəvi qayda budur ki, ən ucuz olan vaxtı alırsınız və ən baha olan vaxtı satırsınız. Amma bu şərait hər zaman mümkün olmaya bilər. Əvvəlcə səhmlərin qiymət cədvəlinə nəzər salaq (adına “Səhm A” nümunəsi deyək):
| Gün | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| Qiymət | 100 | 113 | 110 | 85 | 105 | 102 | 86 | 63 | 81 | 101 | 94 | 106 | 101 | 79 | 94 | 90 | 97 |
Cədvəldən də göründüyü kimi ən ucuz qiymət 8-ci gün, ən baha qiymət isə 2-ci gündə olacaq. Deməli ən ucuza alıb, ən bahaya satmaq mümkün olmayacaq. Bu hal alınmadıqda artıq ən yüksək gəlir gətirə biləcək digər mümkün alternativləri axtarmağa başlamalısınız. Növbəti məntiqli variant budur:
- Səhmin qiymətinin ən ucuz olduğu günü tapırsınız və həmin gündən sona (cədvəldə sağa) doğru ən yüksək qiyməti axtarır və gəliri hesablayırsınız. Deməli, əgər 8-ci gün (63) alıb 12-ci gün (106) satsanız səhm başına gəliriniz 43$ olacaq.
- Səhmin qiymətinin ən baha olduğu günü tapırsınız və həmin gündən əvvələ (cədvəldə sola) doğru ən kiçik qiyməti axtarır və gəliri hesablayırsınız. Bizim nümunəmizdə gəlirin ən yüksək olduğu gün 2-ci gündür. 2-ci gündən əvvəldə ancaq 1 gün olduğundan, deməli biz səhmi 1-ci gün (100) alıb 2-ci gün (113) satmalıyıq və bu zaman səhm başına gəlir 13$ olacaq.
- 1-ci bənddəki gəlir ilə 2-cini müqayisə edirsiniz, hansı gəlir daha böyükdürsə, həmin variantı seçirsiniz. Bizim nümunəmizdə 1-ci bənddəki gəlir daha çoxdur, yəni ən ucuz qiymətə alıb, ondan sonrakı mümkün ən baha qiyməti satsanız daha çox gəlir əldə edəcəksiniz.
Bir az daha aydın təsəvvür olsun deyə Java`da bunun kod nümunəsinə də baxa bilərik, məlumatlar böyüdükcə kod artıq zərurətə çevrilir. Kod təxminən aşağıdakı formada olacaqdır:
public static void findMaximumProfit() {
int[] a = {100, 113, 110, 85, 105, 102, 86, 63, 81, 101, 94, 106, 101, 79, 94, 90, 97};
int length = a.length;
int minValue = Integer.MAX_VALUE, minIndex = 0, maxValue = Integer.MIN_VALUE, maxIndex = 0;
for (int i = 0; i < length; i++) {
if (a[i] < minValue) {
minValue = a[i];
minIndex = i;
} else if (a[i] >= maxValue) {
maxValue = a[i];
maxIndex = i;
}
}
int minMaxIndex = minIndex, minMaxValue = minValue;
for (int i = minIndex; i < length; i++) {
if (a[i] > minMaxValue) {
minMaxValue = a[i];
minMaxIndex = i;
}
}
int maxMinIndex = maxIndex, maxMinValue = maxValue;
for (int i = maxIndex; i >= 0; i--) {
if (a[i] < maxMinValue) {
maxMinValue = a[i];
maxMinIndex = i;
}
}
System.out.println("From min to max: [" + minIndex + "][" + minMaxIndex + "], profit: " + (minMaxValue - minValue));
System.out.println("From max to min: [" + maxIndex + "][" + maxMinIndex + "], profit: " + (maxValue - maxMinValue));
}
Output:
From min to max: [7][11], profit: 43
From max to min: [1][0], profit: 13
İndekslər 0-dan başlayır, əgər üzərlərinə 1 əlavə etsək, eyni günləri alacağıq: [8][12] və [2][1].
Amma bu variant da həmişə ən yaxşı variant olmaya bilər. Fikrimizi əsaslandırmaq üçün fərqli bir qiymət cədvəli üzərindən araşdırmamızı davam etdirək ( bu da “Səhm B” nümunəsi olsun):
| Gün | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| Qiymət | 88 | 104 | 94 | 72 | 86 | 77 | 76 | 103 | 87 | 100 | 96 | 78 | 71 | 84 | 81 | 89 | 93 | 73 | 82 | 97 | 75 |
Yuxarıdakı 3 bəndi yenidən bura tətbiq etsək:
- ən kiçik (ucuz) qiymətdən başlayaraq sona doğru – 13-cü gün $71-dan alırıq və 20-ci gün $97-a satırıq. Bu zaman səhm başına gəlirimiz $26 olur;
- ən böyük (baha) qiymətdən başlayaraq əvvələ doğru – 1-ci gün $88-dan alırıq və 2-ci gün $104-dan satırıq. Bu zaman isə səhm başına gəlirimiz $16 olur;
- 1-ci variant ilə 2-cini müqayisə edirik və daha çox gəlir gətirdiyinə görə 1-ci variantı seçirik.
Deməli, bu varianta görə səhm başına maksimum qazancımız $26 oldu. Amma bu da maksimum deyil, bundan da çox qazana bilərik. Necə?
Əgər 4-cü gün ($72) alıb 8-ci gün ($103) satsaq, səhm başına gəlirimiz $31 olacaq ki, bu da əvvəlkindən $5 çoxdur. Burada məlumatlar az olduğundan biz rəqəmləri bir-bir çıxıb fərqləri müqayisə edib müəyyən nəticə əldə edə bilərik. Bəs məlumatlar minlərlə, milyonlarla olduqda bunu necə tapacağıq?
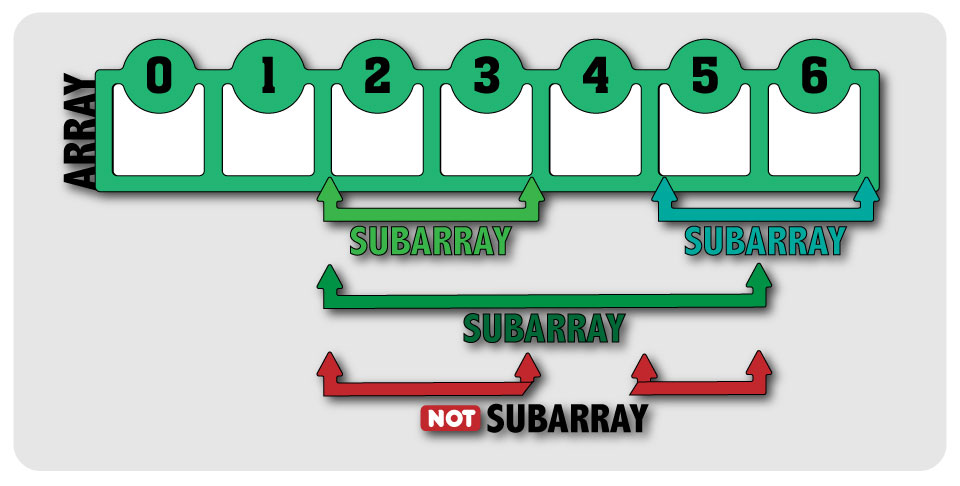
Bu problemi həll etmək üçün maksimum cəmi verən ardıcıl alt-massivin (contiguous subarray) tapılması metodundan istifadə edilir. İngiliscə adı “The maximum-subarray problem” olaraq qeyd olunur. Ardıcıl alt-massiv dedikdə massivin hər hansı bir hissəsi nəzərdə tutulur, amma bir şərtlə ki, alt-massivdəki indekslər mütləq bir-birinə qonşu olmalıdır, arada qırılma olmamalıdır, yəni ardıcıl indekslərdən ibarət olmalıdır. Şəkildən daha aydın görsənir1:
Bütövlükdə massivin özü də ardıcıl alt-massiv ola bilər. Məsələn, massivin bütün elementləri müsbətdirsə, maksimum cəmi verən ardıcıl alt-massiv (bundan sonra maksimum alt-massiv) elə bütövlüklə həmin massivin özüdür. Maksimum alt-massivin tapılması massivin elementlərinin içərisində mənfi dəyərlər olduqda aktual olur. Əgər mənfi dəyər yoxdursa, istənilən halda maksimum cəm bütün elementlərdən ibarət olan cəm olur və bu da massivin özüdür.
Əgər mənfi dəyərlər olarsa, maksimum alt-massiv necə hesablanır?
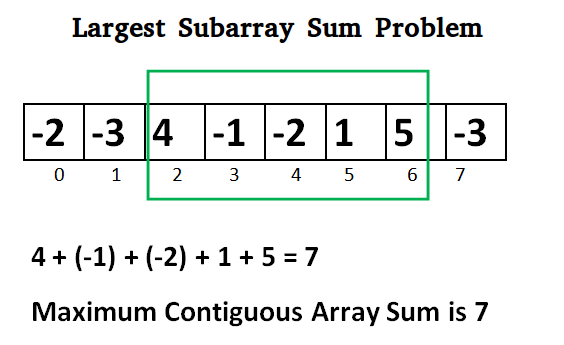
Maksimum alt-massivin neçə elementdən ibarət olması, hansı indeksdən başlaması, hansı indeksdə bitməsi ilə bağlı hər hansı bir tələb yoxdur. Sadəcə indekslər yanaşı olsun və həmin indeks aralığında olan elementlərin cəmi, bütün digər mümkün alternativlər ilə müqayisədə maksimum olsun. Daha açıqlayıcı olsun deyə şəkil üzərindən də baxaq (“Massiv C” nümunəsi)2:
Göründüyü kimi şəkildə 8 elementdən ibarət bir massiv verilib. 2-ci indeksdən başlayaraq 6-cı indeks də daxil olmaqla (A[2.. 6]) bizim maksimum alt-massivimizdir. Əgər biz 2-ci indeksi götürmüşüksə, 3-cü və 4-cü indekslərin mənfi dəyər almasına baxmayaraq, alt-massivin ardıcıl (contiguous) olması şərtinin ödənməsi üçün onları da mütləq maksimum alt-massivə daxil etməliyik.
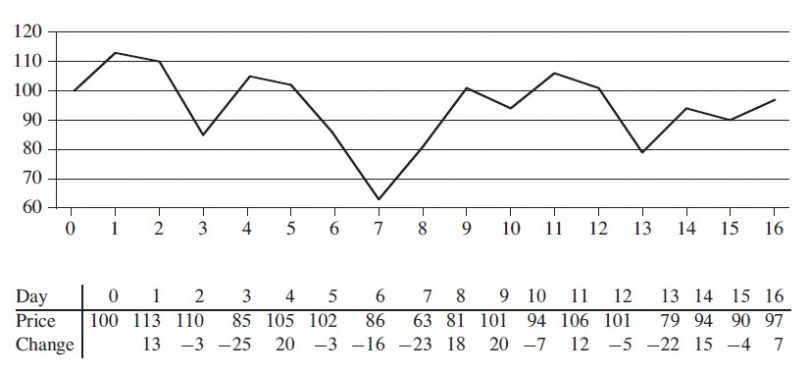
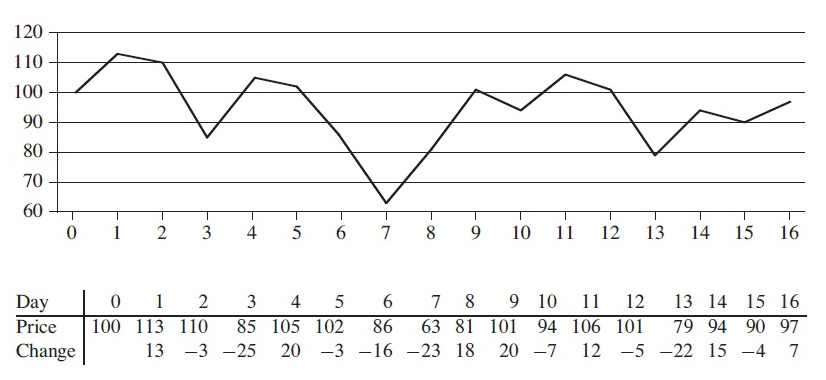
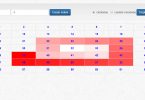
Tutaq ki, biz maksimum alt-massivi tapdıq. Bəs onu yuxarıda qeyd etdiyimiz səhm alqı-satqısı probleminə necə tətbiq edəcəyik? İzaha “Introduction to Algorithms” kitabından haqqında bəhs etdiyimiz mövzu ilə əlaqəli bir şəkil ilə davam edək3:
Yuxarıda qeyd etdiyimiz məlumatlar burada da mövcuddur, amma əsas fərq odur ki, burada “Change” sətri əlavə edilib. Bu sətir cari gün ilə ondan əvvəlki gün arasında olan qiymət dəyişikliklərini göstərir. Əgər müsbət ədəddirsə, deməli dünənki gün ilə müqayisədə bugün qiymət artıb, mənfi ədəddirsə, azalıb. Həmçinin artımın və ya azalmanın məbləğini də görürük. Bu dəyişiklik siyahısı bizə niyə görə lazımdır?
Çünki biz qeyd etdik ki, massivin bütün elementləri müsbət olarsa, maksimum alt-massiv problemi elə də önəmli olmur. Qiymətlər (Price) hamısı müsbət ədədlər olduğundan, onlardan istifadə edərək maksimum alt-massiv probleminə yanaşsaq nəticə əldə edə bilməyəcəyik. Amma dəyişiklik (change) həm müsbət, həm də mənfi ədədlərdən ibarət olduğuna görə problemin həlli üçün əsas bu məlumatlardan istifadə edəcəyik və massivimiz aşağıdakı kimi olacaq:
// index 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
int[] change = {13, -3, -25, 20, -3, -16, -23, 18, 20, -7, 12, -5, -22, 15, -4, 7};
Bu massivi A[0.. 15] kimi işarə etsək o zaman bizim maksimum alt-massivimiz A[7.. 10] olacaq (necə tapılması alqoritmlərinə aşağıda baxacağıq). Yəni 7-ci indeksdən 10-cu indeks də daxil olmaqla elementlərin cəmi maksimum cəmdir:
maksimum cəm = 18 + 20 + (-7) + 12 = 43
Bu maksimum cəm səhm başına götürə biləcəyimiz maksimum gəliri bildirir. Fikir verdinizsə, birinci nümunədə də qeyd etmişdik ki, səhm başına götürə biləcəyimiz maksimum gəlir $43 idi. Yəni qısacası maksimum cəm nə qədərdirsə, götürə biləcəyimiz maksimum gəlir də o qədər ola bilər. Yuxarıdakı nümunədə $26 əvəzinə $31 qazana biləcəyimizi də maksimum cəmin sayəsində təyin etmişdik.
Bəs maksimum alt-massivə görə hansı gün alıb, hansı gün satacağımızı necə biləcəyik?
A[7.. 10] – burada 7-ci indeksdən bir əvvəlki indeks alacağımız gün, 10-cü indeks isə satacağımız gündür. Yəni 7-ni begin, 10-u end kimi qəbul etsək:
alma vaxtı = begin -1;
satma vaxtı = end;
Bu yanaşmaya əsasən bizim alma vaxtımız 6-cı indeks (-23) 7-ci günə uyğun gəlir və satma vaxtımız 10-cu indeks (12) isə 11-ci günə uyğun gəlir. Şəkildə indekslər sıfırdan başladığına görə bu dolayı yolla 8-ci və 12-ci günlər deməkdir. Və bununla da alqı-satqı ilə bağlı yazının “Səhm A” nümunəsində qeyd etdiyimiz üsulu təsdiqləmiş olduq.
İndi isə maksimum alt-massivlə bağlı qeyd etdiklərimizin hamısının əyani şəkildə hesablanmasına baxacağıq və bunun üçün hansı alqoritmlərdən, yöntəmlərdən istifadə olunur onları görəcəyik.
Maksimum alt-massivin tapılması üsulları
Bu məqalədə maksimum alt-massivin tapılması üçün əsas 3 üsula baxacağıq:
- Sadə üsulla həll variantı;
- “Divide and conquer” yanaşmasından istifadə edərək rekursiv metodla həll variantı;
- Kadane alqoritmi ilə həll variantı.
Əslində səhmlə bağlı nümunə kitabda “Divide-and-Conquer” bölməsində verilib və orada ancaq 2-ci həll variantı göstərilib, məqsəd isə “divide-and-conquer” yanaşmasının avantajlarını oxucuların diqqətinə çatdırmaqdır. Amma mövzunu oxuyub araşdırarkən digər həll üsullarına da rast gəldim və bu həll üsullarının bir-biri ilə müqayisəli şəkildə verilməsinin alqoritm mövzusunun önəmini, mahiyyətini, niyə görə vacib olduğunu göstərmək baxımından faydalı olacağını düşünürəm. Əslində bu 3 metodun üçü də mahiyyət baxımından eyni işi görür və üçü də bizə lazım olan eyni nəticəni verir. Yəni bunlardan birini bilməklə problemimizi həll edə bilərik. Bəs onda niyə görə fərqli üsullar mövcuddur? Səbəb nədir? Bu suallara aydınlıq gətirmək üçün hər 3 metod haqqında qısaca yazmağa və fərqlərini göstərməyə çalışacam.
-
Sadə üsulla həll variantı
Bu üsul üçün iç-içə 2 dövr istifadə edirik. Əvvəlcə kodunu yazaq, sonra onun üzərindən izah edək:
public static int[] findMaximumSubarrayWithSimpleWay(int[] arr) {
int maxSum = Integer.MIN_VALUE, sum = 0;
int left = 0, right = 0;
for (int i = 0, length = arr.length; i < length; i++) {
sum = 0;
for (int j = i; j < length; j++) {
sum += arr[j];
if (sum > maxSum) {
maxSum = sum;
left = i;
right = j;
}
}
}
return new int[]{left, right, maxSum};
}
maxSum-ın dəyərini sıfır deyil, Integer.MIN_VALUE veririk (0-cı indeksin dəyərini də mənimsətmək olar). Çünki elə hal ola bilər ki, massivin bütün elementləri mənfi ola bilər, o halda maksimum alt-massiv ən böyük mənfi dəyərə sahib olan element olacaq.
İşləmə məntiqi çox sadədir. Hər dəfə i-ci elementdən başlayır və massivin sonuna qədər bütün elementləri cəmləyir. Əgər maksimum alt-massivimizin A[left.. right] olduğunu fərz etsək, o zaman left dəyişəninin dəyəri hər zaman i-yə bərabərdir, stabildir. Qalır right indeksimizi tapmaq. i-ci indeksdən sona doğru maksimum cəm hansı indeksdə alınırsa, həmin indeks də right indeksimiz olur. Dediklərimizi əyani olaraq görmək üçün nümunə kimi “Massiv C”-ni götürək və proseslərin necə baş verməsinə həmin massiv üzərindən baxaq:
int[] arr = {-2, -3, 4, -1, -2, 1, 5, -3};
[i=0] (-2) + (-3) + 4 + (-1) + (-2) + 1 + 5 + (-3) A[0.. 6],maxSum: 2
[i=1] (-3) + 4 + (-1) + (-2) + 1 + 5 + (-3) A[1.. 6],maxSum: 4
[i=2] 4 + (-1) + (-2) + 1 + 5 + (-3) A[2.. 6],maxSum: 7
[i=3] (-1) + (-2) + 1 + 5 + (-3)
[i=4] (-2) + 1 + 5 + (-3)
[i=5] 1 + 5 + (-3)
[i=6] 5 + (-3)
[i=7] -3
Hər dəfə elementlər cəmləndikdən sonra maxSum dəyəri ilə müqayisə edilir. Əgər maxSum dəyərindən böyük olarsa, həmin cəm maxSum dəyişəninə mənimsədilir. Böyük deyilsə heç bir əməliyyat edilmir və elementlərin cəmlənməsinə davam edilir. İçdəki dövrdən çıxdıqdan sonra sum dəyişəni sıfırlanır, amma maxSum olduğu kimi qalır. Növbəti i indeksindən başlayaraq elementlərin cəmlənməsi davam edir və maxSum ilə müqayisə aparılır. Bu proses i indeksi massivin son elementini də yoxladıqdan sonra bitir.
İlk baxışdan sadə və rahat görsənir. İkinci üsulun kodlaşdırılmasını görsəniz qəti şəkildə bu kodu istifadə etməyi tərcih edərsiniz 🙂 Çünki bu kodun nə iş gördüyünü başa düşmək ikinciyə nisbətən çox-çox asandır. Amma necə deyərlər, “hər gözəlin bir eybi var”. Bu kodun güclü bir dezavantajı var və bu dezavantaj işləmə müddəti ilə əlaqəlidir. Kiçik ölçülü massivlərdə bu müddət o qədər də gözə çarpmır. Amma məlumatın həcmi minlərlə, milyonlarla olduqda, bir sözlə müsbət sonsuzluğa yaxınlaşdıqca bu müddət kəskin şəkildə özünü büruzə verir. Alqoritmlərdə ən önəmli iki faktor: işləmə müddəti və istifadə edilən yaddaş sahəsidir. Alqoritm kitablarında “complexity” deyilən anlayış var, türkcə kitablarda “karmaşıklık” kimi tərcümə olunur. Biz də alternativ olaraq müvəqqəti termin kimi “performans” sözünü istifadə edək. Bu termindən kodu analiz etmək üçün istifadə edirlər və bu analizin nəticəsinə görə kodun performansını dəyərləndirirlər. Yekunda bu kodun işləmə müddətini bildirir. Bu mövzu ilə bağlı Şadi Evren Şekerin “Koddan Karmaşıklık Analizi Yapılması” adlı youtube videosu var, təsəvvür olması üçün həmin videoya baxa bilərsiniz (Qısaca haşiyəyə çıxaraq deyim ki, ümumiyyətlə, bu adamın youtube kanalı çox faydalıdır, alqoritmlə bağlı kitabdan oxuduğum, amma qaranlıq qalan mövzuların bir neçəsinə həmin kanaldan baxmışam, çox yaxşı izah edir. Sizin də izləməyinizdə fayda var). Videoda da qeyd edildiyi kimi kodun performansını Böyük O (Big O) ilə işarə edirlər. Böyük O ilə işarə edəcək olsaq bizim kodumuzun performansı O(n2) –dir. Bu bizim kodumuzun işləmə müddətini xarakterizə edən göstəricidir. İşləmə müddəti deyildikdə saniyə, millisaniyə və ya hər hansı bir vaxt intervalı nəzərdə tutulmur. İşləmə müddəti deyildikdə alqoritm başlayandan bitənədək yerinə yetiriləcək əməliyyatların (toplama, çıxma, çapetmə və s.), addımların sayı nəzərdə tutulur.
The running time of an algorithm on a particular input is the number of primitive operations or “steps” executed.
“Introduction to Algorithms”, 3-cü nəşr, səhifə 25
O(n2) o deməkdir ki, məlumatların həcmi sonsuz dövrə yaxınlaşdıqca alqoritmin böyümə mərtəbəsi (rate of growth) kvadratik olaraq artır. Yəni daha anlaşıqlı olması üçün loru dildə belə deyə bilərik: massiv 10 elementdən ibarətdirsə, 100 əməliyyat, 100 elementdən ibarətdirsə, 10000 əməliyyat yerinə yetiriləcək və s. Kvadratik artma budur və bu da yaxşı nəticə hesab edilmir. Adətən iç-içə istifadə edilən dövrlər üçün ən pis performans və ya “worst-case” O(n2) hesab olunur və məlumatın həcmi artdıqca işləmə müddəti xeyli uzanır. O səbəbdən dövrlərin mümkün qədər iç-içə istifadə edilməməsi tövsiyə edilir. Məqalənin sonunda işləmə müddəti ilə bağlı bu üsulun digər üsullarla müqayisəsi veriləcək, o zaman fərqi əyani olaraq görəcəksiniz.
-
“Divide and conquer” yanaşması ilə həll variantı
“Divide and conquer” ifadəsini dilimizə “parçala və idarə et” yaxud “parçala və hökm sür” kimi tərcümə edə bilərik. Yanaşmanın əsas qayəsi ondan ibarətdir ki, böyük problemlər kiçik hissələrə bölünür, çünki problemləri kiçik ikən həll etmək daha asandır. Kiçik problemləri həll etdikcə yenidən onları hissə-hissə birləşdirməyə başlayırıq. Ən son hissələr birləşdirildikdən sonra artıq böyük problem həll edilmiş olur. “Divide and conquer” yanaşmasının tətbiq edildiyi ən klassik alqoritmlərdən biri Merge sort alqoritmidir, bu mövzu barədə daha geniş şəkildə Merge sort alqoritmi ilə bağlı məqalədə yazmağı planlaşdırıram. Bu məqalə artıq kifayət qədər böyük alındı, bir az da “divide and conquer” haqqında yazsaq həcm daha da böyüyəcək. Ona görə də əsas hissəni digər məqaləyə saxlayıram, burada vacib bir-iki məqama toxunacam. Əgər zərurət yaranarsa, təkrar qayıdıb bu hissəyə əlavələr edərəm.
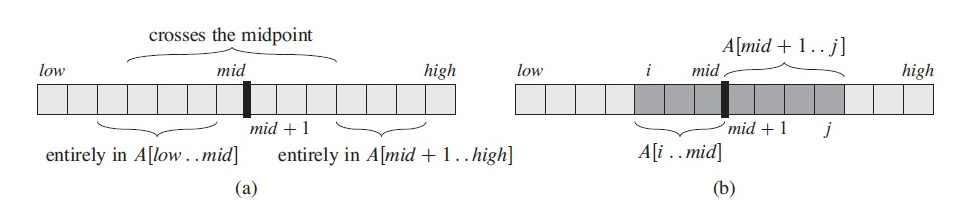
“Divide and conquer” yanaşması massivi adətən 2 mümkün bərabər hissəyə bölməyi təklif edir. Aşağıdakı şəkildən göründüyü kimi əgər mid bizim massivin mərkəz nöqtəsi olsa, o zaman A[low.. mid] bizim sol alt-massivimiz A[mid+1.. high] isə sağ alt-massivimiz olacaq. Əgər A[i.. j] bizim maksimum alt-massivimiz olarsa, maksimum alt-massivlə bağlı aşağıdakı 3 haldan mütləq biri doğrudur4:
- tamamilə A[low.. mid] massivinin daxilindədir,
low ≤ i ≤ j ≤ mid; - tamamilə A[mid+1.. high] massivinin daxilindədir,
mid < i ≤ j ≤ high; - bu iki massivin birləşməsindədir, yəni
low ≤ i ≤ mid < j ≤ high.
Qısaca, yazacağımız kodun görəcəyi iş bu olacaq:
- rekursiya vasitəsilə massivi 2 yerə böləcək;
- sol tərəfdəki massiv üçün maksimum cəmi hesablayacaq;
- sağ tərəfdəki massiv üçün maksimum cəmi hesablayacaq;
- sol və sağ massivin birləşməsindən yaranan cəmi hesablayacaq;
- sol, sağ və birləşmədən yaranan cəmləri müqayisə edəcək;
- cəmi böyük olan massivi seçəcək.
Kodumuzu yazaq:
public static int[] findMaximumSubarray(int[] a, int low, int high) {
if (low == high) return new int[]{low, high, a[low]};
int mid = (low+high)/2;
int[] left = findMaximumSubarray(a, low, mid);
int[] right = findMaximumSubarray(a, mid+1, high);
int[] cross = findMaxCrossingSubarray(a, low, mid, high);
if(left[2] >= right[2] && left[2] >= cross[2])
return left;
else if (right[2] >= cross[2])
return right;
else
return cross;
}
private static int[] findMaxCrossingSubarray(int[] a , int low, int mid, int high) {
int sum = 0, leftSum = Integer.MIN_VALUE, rightSum = Integer.MIN_VALUE;
int maxLeft = -1, maxRight = -1;
for (int i = mid; i >= low; i--) {
sum += a[i];
if (leftSum < sum) {
leftSum = sum;
maxLeft = i;
}
}
sum = 0;
for (int j = mid + 1; j <= high; j++) {
sum += a[j];
if (rightSum < sum) {
rightSum = sum;
maxRight = j;
}
}
return new int[]{ maxLeft, maxRight, (leftSum + rightSum)};
}
Kodun strukturu nisbətən qəlizdir, necə işləməsini başa düşmək üçün ilk öncə rekursiv metodun necə işləməsini mütləq bilmək lazımdır. Merge sort alqoritmində də rekursiv metod təxminən bu formada istifadə edilir, həmin məqalədə bunun izahını verməyə çalışacam İnşallah. Rekursiv metodlara giriş ilə bağlı əlavə bir məqalə də planlaşdırmışam. Sağlıq olsa, onu da paylaşacam.
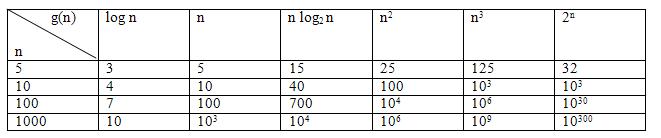
Əvvəlki üsul ilə müqayisədə bu üsulun necə işləməsini başa düşmək, kodlaşdırmaq qəliz olsa da, performans baxımından çox güclü avantajı var. Əvvəlki üsulun performansının O(n2) olduğunu demişdik, bu üsulun performansı isə O(nlogn)-dir. Yəni funksiya loqarifmik olaraq böyüyür, bu da kvadratik böyüməyə nisbətən çox yaxşı nəticədir.
Qeyd. Loqarifmanı unudanlar üçün qısa xatırlatma edim. Bizim nümunəmiz əsası 2 olan loqarifmadır və belə hesablanır:
log2n = x --> 2x = n, n=10 üçün x = ~3.3, n=100 üçün x = ~6.6
-
Kadane alqoritmi
Çox maraqlı alqoritmdir və super işləyir. Təsəvvür edin 1-ci üsul üçün yazdığımız kodda xırda dəyişikliklər etməklə dövrün birindən imtina edirik və performans baxımından həmin kodu xeyli qabaqlamış oluruq. Performansı O(n)-dir, yəni sonsuz dövrə yaxınlaşdıqca alqoritmin böyümə mərtəbəsi (growth rate) xətti olaraq artır. Bu da digər 2 üsulla müqayisədə performans baxımından ən yaxşı nəticədir. Ümumiyyətlə isə Kadane alqoritmi maksimum alt-massivin tapılması üçün ən yaxşı alqoritm hesab edilir.
Əvvəlcə kodunu yazaq, sonra kod üzərindən izah edək:
public static int[] findMaximumSubarrayWithKadane(int arr[]) {
int maxSum = Integer.MIN_VALUE, sum = 0;
int left = 0, right = 0, next = 0;
for (int i = 0, length = arr.length; i < length; i++) {
sum += arr[i];
if (maxSum < sum) {
maxSum = sum;
left = next;
right = i;
}
if (sum < 0) {
sum = 0;
next = i + 1;
}
}
return new int[]{left, right, maxSum};
}
Alqoritmin ideyası ondan ibarətdir ki, cəmi müsbət ədəd verən ardıcıl (contiguous) alt-massivləri axtarır, başqa cür desək massivi qeyd etdiyimiz şərti ödəyən alt-massivlərə bölür. Sonra bu alt-massivlərin hər biri üçün maksimum cəmi hesablayır və bu maksimum cəmlər arasında müqayisə aparır. Və nəticə olaraq da bizə bildirir ki, maksimum alt-massiv maksimum cəmi verən alt-massivin daxilindədir.
Alqoritmi bu formada, nəzəri sözlərlə başa düşmək bir az çətin olacaq, ona görə də effektiv ola biləcək bir şeylər fikirləşmək zərurəti hiss elədim. Son olaraq nümunə bir massiv götürüb və koda print sətirləri əlavə edərək əyani bir şey göstərmək qərarına gəldim. Ümid edirəm, başa sala biləcəm 🙂
Kodumuzu yazaq, icra edək və çıxış görüntüsünə baxaq:
public static void main(String[] args) {
int[] arr = {12, -7, -3, -3, 12, -1, -8, -4, 6, -3, 4, 5, -7, 9, -2};
int maxSum = Integer.MIN_VALUE, sum = 0;
int left = 0, right = 0, next = 0;
for (int i = 0, length = arr.length; i < length; i++) {
sum += arr[i];
if (next == i) System.out.print("[" + next + ".. ");
if (maxSum < sum) {
maxSum = sum;
left = next;
right = i;
}
if (sum < 0) {
sum = 0;
next = i + 1;
System.out.println(i + "] maxSum: " + maxSum);
}
}
System.out.println(arr.length - 1 + "] maxSum: " + maxSum);
System.out.printf("\n[%d.. %d] maxSum: %d <-- maximum subarray\n", left, right, maxSum);
}
Output:
[0.. 3] maxSum: 12
[4.. 7] maxSum: 12
[8.. 14] maxSum: 14
[8.. 13] maxSum: 14 <-- maximum subarray
Başlayaq izahına. Qeyd etdik ki, cəmi müsbət ədəd verən ardıcıl alt-massivlər axtarılır. Sıfırıncı indeksdən etibarən elementləri cəmləməyə başlayırıq:
12 --> 12 maxSum [indeks=0]
12 + (-7) --> 5
5 + (-3) --> 2
2 + (-3) --> -1 [indeks=3]
Artıq 3-cü indeksdə qeyd etdiyimiz tələb pozuldu, cəm mənfi ədəd oldu. Bu səbəbdən sum sıfırlanır və 4-cü indeksdən başlayaraq cəmi müsbət ədəd verən növbəti ardıcıl alt-massiv axtarılır.
12 --> 12 [indeks=4]
12 + (-1) --> 11
11 + (-8) --> 3
3 + (-4) --> -1 [indeks=7]
7-ci indeksdə qeyd edilən tələb pozuldu və [4..7] növbəti alt-massivimiz oldu. Cəmlərin heç biri 12-dən böyük olmadığı üçün maxSum yenilənmədi. Hələ ki, maksimum alt-massivimiz [0.. 0]-dır. Keçək növbəti alt-massivimizi axtarmağa, başlanğıc indeksimiz 8 olacaq və həmçinin cəmimiz sıfırlanacaq:
6 --> 6 [indeks=8]
6 + (-3) --> 3
3 + 4 --> 7
7 + 5 --> 12
12 + (-7) --> 5
5 + 9 --> 14 maxSum [indeks=13]
14 + (-2) --> 12 [indeks=14]
Dövrümüz başa çatdı və gördüyünüz kimi qeyd edilən tələbləri ödəyən 3 alt-massivimiz oldu. Maksimum cəmi 3-cü alt-massivdə əldə etdik, deməli bizim maksimum alt-massivimiz bu alt-massivin daxilindədir. Maksimum alt-massiv üçün başlanğıc yaxud left indeks həmişə tapılan alt-massivlərin başlanğıc indeksləri ilə üst-üstə düşür, dəyişmir. Sadəcə son indeksi təyin etməliyik. maxSum ən böyük qiymətinə 13-cü indeksdə çatdığına görə bu indeks bizim right indeksimiz olacaq. Və beləliklə maksimum alt-massivimiz [8.. 13], cəmimiz isə 14 olacaq.
Sonda hər üç üsul üçün yazdığımız kodları bir class daxilində cəmləşdirək və işləmə vaxtlarını müqayisə edək:
package az.mm.algoritms.maximumsubarray;
import java.util.ArrayList;
import java.util.Arrays;
import java.util.List;
import java.util.Random;
public class MaximumSubarray {
private static long start, duration;
public static void main(String[] args) {
int[] priceOfDays, change;
/*
// "Səhm A" numunesi uchun
priceOfDays = new int[]{100, 113, 110, 85, 105, 102, 86, 63, 81, 101, 94, 106, 101, 79, 94, 90, 97};
change = new int[]{13, -3, -25, 20, -3, -16, -23, 18, 20, -7, 12, -5, -22, 15, -4, 7};
// "Səhm B" numunesi uchun
priceOfDays = new int[]{88, 104, 94, 72, 86, 77, 76, 103, 87, 100, 96, 78, 71, 84, 81, 89, 93, 73, 82, 97, 75};
change = new int[]{16, -10, -22, 14, -9, -1, 27, -16, 13, -4, -18, -7, 13, -3, 8, 4, -20, 9, 15, -22};
// Ashagidaki metodlarla yuxaridaki numunelere benzer numuneler yaradib testler ede bilersiniz
priceOfDays = createUniqueIntArray(30, 100, 70);
change = createDifferencesArray(priceOfDays);
*/
// boyuk hecmli test uchun unique olma shertini qaldiracam, chunki contains metodu xeyli vaxt alacaq
priceOfDays = createUniqueIntArray(1_000_000, 5000, -5000);
System.out.println("1st way");
start();
print(findMaximumSubarrayWithSimpleWay(priceOfDays));
end();
System.out.println("2nd way");
start();
print(findMaximumSubarray(priceOfDays, 0, priceOfDays.length-1));
end();
System.out.println("3rd way");
start();
print(findMaximumSubarrayWithKadane(priceOfDays));
end();
}
// 1st way - simple way using nested loops, complexity O(n^2)
public static int[] findMaximumSubarrayWithSimpleWay(int[] arr) {
int maxSum = Integer.MIN_VALUE, sum = 0;
int left = 0, right = 0;
for (int i = 0, length = arr.length; i < length; i++) {
sum = 0;
for (int j = i; j < length; j++) {
sum += arr[j];
if (sum > maxSum) {
maxSum = sum;
left = i;
right = j;
}
}
}
return new int[]{left, right, maxSum};
}
// 2nd way - divide and conquer, complexity O(nlogn)
public static int[] findMaximumSubarray(int[] a, int low, int high) {
if (low == high) return new int[]{low, high, a[low]};
int mid = (low+high)/2;
int[] left = findMaximumSubarray(a, low, mid);
int[] right = findMaximumSubarray(a, mid+1, high);
int[] cross = findMaxCrossingSubarray(a, low, mid, high);
if(left[2] >= right[2] && left[2] >= cross[2])
return left;
else if (right[2] >= cross[2])
return right;
else
return cross;
}
private static int[] findMaxCrossingSubarray(int[] a , int low, int mid, int high) {
int sum = 0, leftSum = Integer.MIN_VALUE, rightSum = Integer.MIN_VALUE;
int maxLeft = -1, maxRight = -1;
for (int i = mid; i >= low; i--) {
sum += a[i];
if (leftSum < sum) {
leftSum = sum;
maxLeft = i;
}
}
sum = 0;
for (int j = mid + 1; j <= high; j++) {
sum += a[j];
if (rightSum < sum) {
rightSum = sum;
maxRight = j;
}
}
return new int[]{ maxLeft, maxRight, (leftSum + rightSum)};
}
// 3rd way - Kadane's Algorithm, complexity O(n)
public static int[] findMaximumSubarrayWithKadane(int arr[]) {
int maxSum = Integer.MIN_VALUE, sum = 0;
int left = 0, right = 0, next = 0;
for (int i = 0, length = arr.length; i < length; i++) {
sum += arr[i];
if (maxSum < sum) {
maxSum = sum;
left = next;
right = i;
}
if (sum < 0) {
sum = 0;
next = i + 1;
}
}
return new int[]{left, right, maxSum};
}
private static int[] createUniqueIntArray(int length, int maxValue, int minValue){
List<Integer> list = new ArrayList<>();
for(int i=0; i<length; i++){
int random1 = new Random().nextInt((maxValue - minValue) + 1) + minValue;
int random2 = new Random().nextInt(9) + 1;
int value = random1 + random2;
// if(!list.contains(value))
list.add(value);
}
int[] arr = list.stream().mapToInt(i->i).toArray();
System.out.println("Array length = " + arr.length + "\n");
return arr;
}
private static int[] createDifferencesArray(int arr[]){
int differencesArr[] = new int[arr.length-1];
for(int i=0, length = arr.length-1; i<length; i++){
differencesArr[i] = arr[i+1]-arr[i];
}
return differencesArr;
}
private static void print(int[] arr){
System.out.println(Arrays.toString(arr));
}
private static void start(){
start = System.currentTimeMillis();
}
private static void end(){
duration = System.currentTimeMillis()-start;
System.out.println("Duration: " + duration + "ms\n");
}
}
Mənim lokal kompyuterimdə random olaraq yaradılmış 1000 və 1_000_000 elementdən ibarət olan massivlər üçün nəticə belə oldu:
Array length = 1000
1st way
[231, 415, 78276] Duration: 4ms
2nd way
[231, 415, 78276] Duration: 1ms
3rd way
[231, 415, 78276] Duration: 0ms
Array length = 1000000
1st way
[341890, 979423, 6103244] Duration: 517102ms
2nd way
[341890, 979423, 6103244] Duration: 65ms
3rd way
[341890, 979423, 6103244] Duration: 6ms
Gördüyünüz kimi n-in qiyməti (elementlərin sayı) artdıqca işləmə müddətlərində olan fərqlər özünü kəskin büruzə verir. O(n), O(nlogn) və O(n2)-nın əhəmiyyəti burada özünü göstərir. Cədvəldən də bunu təxmin edə bilərsiniz:
Beləcə məqalənin sonuna gəldik. Deyəsən bu indiyə qədər yazdığım ən böyük məqalə oldu. Yazıda “giriş-çıxış”lar çox olduğuna görə nələrsə gözümdən qaça bilər. Zəhmət olmasa diqqətinizi çəkən hər hansı bir xəta görsəniz bildirin. Ümid edirəm faydalı olacaqdır. Uğurlar!
Github link:
https://github.com/mmushfiq/MaximumSubarray
1 https://www.linkedin.com/pulse/kadanes-algorithm-mustafa-bedir-tapkan
2 http://www.geeksforgeeks.org/largest-sum-contiguous-subarray/
3 “Introduction to Algorithms” (MIT Press), 3-cü nəşr, səhifə 68
4 “Introduction to Algorithms” (MIT Press), 3-cü nəşr, səhifə 71
[…] real problemlər üzərində tətbiqi maraqlandırır. Blogda bu səpkidə daha öncə bir məqalə paylaşmışam, səhm alqı-satqısı məsələsində Kadane alqoritminin necə tətbiq edilməsi […]